望遠鏡や双眼鏡の収差について(1)

先日、弊社の窓から虹が出ているのが見られました。虹は太陽光が空気中にある小さな水滴内を通る際に太陽光が分散する事によって見られる自然現象です。よく、この自然現象を説明するのにプリズムを使った虹を作る実験が知られています。プリズムを透過した光は赤や黄、緑、青色など（スペクトル）に分散し、太陽光はこれらの色の光が集合したものである事が解ります。プリズムを使った実験があまりにも有名ですから、プリズムでなければ光は分散しないように思われていますが、実はどのようなレンズでも起こりうる現象なのです。 　光はある物質を透過する際に屈折する事が知られていて、波長によって異なる屈折をします。波長によって異なる屈折をすると言うことは、色によって違う進み方をすると言うことです。一般的には波長の短い青色が強く屈折し、波長の長い赤色は弱く屈折します。すなわち、空気中の水滴内で屈折した太陽光が色によって違う進み方をする、光の分散が目に見えるようになったものが虹なのです。

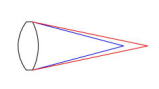収差を全く補正していない左の図のような口径50mmのBK7凸 レンズ（+106mm・-83mm厚さ9.2mm）では、青色（436nm）と赤色（656nm）の焦点距離の差は約2mmとなり、球面収差も補正されていません。これを対物レンズとして使用することはできま せん。

プリズム同様、凸レンズでも凹レンズでも分散は起こることになります。たとえば、弊社の単眼鏡では最低でも7個のレンズが使われていますが、光学機器の分野ではそれぞれのレンズを透過する光が分散して、最終的に実物とは違う像に見える事を色収差があると言います。これら光学機器全般は波長（色）によって異なる屈折をする光をレンズ形状や材質、構成により目立たないようにして、見える像を実物に近づけています。これを「色収差を補正する」と言います。 　収差にはこの色収差のほかにレンズの特性が原因するものや様々な種類のものがあり、通常すべての収差が完全にその光学機器から無くなる事はありません。これを残存収差と呼び、良い光学機器とは収差補正により残存収差が少ないものと言い換える事ができます。光学機器の性能を左右する代表的な収差が下記のようなものです。

色収差	光が分散する事が原因となる収差
球面収差	レンズ面が球面である事が原因となる収差
コマ	同レンズ面の違う場所を透過した光線が違う倍率で結像する事が原因となる収差
非点収差	一方向に鮮鋭な像が他方向でボケた像になる事が原因となる収差
像面湾曲	透過した光線が湾曲、横にした皿のようにお椀型に結像する事
歪曲	球面収差と同原因で、中心光線と周辺光線の屈折過不足が原因となる収差

---

収差について(2)

「収差について（1）」ではレンズ特有の収差を簡単にご説明いたしました。この収差は製造したい望遠鏡の大きさなどから、レンズ設計により収差を最小にする事によって、見える像を実物に近づけました。しかし、必ず良い設計をしても実物像に近づくものではありません。良い部品加工も必要です。下記はレンズの不良加工の例で、上方の1枚の凸レンズの左右の両はじをご覧ください。左側と右側とではレンズ幅が違っています。レンズ研磨の不良で、このレンズでは光線は曲がってしまいますし、収差が出てしまいます。左下側のレンズでは、同じ曲率の凸レンズと凹レンズを組み合わせるときに曲がってしまっている例です。また右下のプリズムでは角度が問題となります。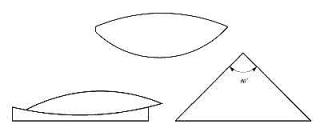 　国内で材料を調達して研磨や加工する場合は下記ほどひどい物は無いのですが、やはり微妙に存在することは確かです。そこで組立職人の経験が生きてきます。例えば直角プリズムの90度を彼らは簡単に、それも誤差30秒ほどを見分けてしまいます。このプリズムの角度は90度より30秒以上大きい、小さいなどです。そして、このレンズとこのレンズを組み合わせれば、光線の直進性が保たれ、収差が少なくなると考えて組み立てるのです。

部品加工はレンズだけではありません。ボディやレンズの金枠などの機械加工です。当然のことですが、この機械加工もレンズ加工と同様に重要となります。いくら良い設計で、良い加工されたレンズでも、そのレンズを入れる枠やボディが曲がっていたり、加工が狂っていれば意味がありません。時間があるとき、研究の為に他社製の望遠鏡や双眼鏡を分解することがあるのですが、今でも感銘を受けた双眼鏡を思い出す事があります。その双眼鏡は西ドイツ時代のCARL ZEISS 8X30で、分解に時間がかかったのですが、組立、光軸調整がとても楽だったのです。レンズもさることながら、一つ一つの部品の機械加工の精度が非常に高く、そのため組立が楽だったのです。また、隅々まで処理がなされていて、「そこまでやるか？」と感じました。でもその分、お値段も非常に高かった事が思い出されます。

---

望遠鏡・単眼鏡や双眼鏡などの倍率について

---

次のようなお問合せをよくお客様からいただきます。「私の視力（右*.*左*.*）でメガネを使用しないでこの双眼鏡を使用したいのですが、使用できますか？」というものです。このような場合、弊社ではお客様が現在使用されているメガネの度数（ディオプタ−）を伺っております。大きく分ければメガネも双眼鏡もレンズを使用した光学機器で、実は視力とはあまり関係ありません。光学ではこのディオプタ−（※）を「D」という記号であらわします。 　たとえば、500�oの焦点距離を持つ凹レンズをかけると遠くの物がよく見える眼の事を「-2Dの近視」と言います。双眼鏡や単眼鏡は規格上、少なくとも「-4D」までを補正できるようになっております（機種によってはもっと補正できるものもございます）。また、弊社ではご依頼いただければ機種にもよりますが調整して、お客様のご要望にできるだけお応えするようにいたしております。 　考え方を変えれば-2Dのメガネをかけると補正されて遠くの物がよく見えると言うことは、眼の中に+2Dの凸レンズがあると想定できます。裸眼で近いところがよく見えるのもそのためです。すなわち-2Dの近視とは-2Dの凹レンズをかけると眼の中にある仮想の凸レンズの作用が打ち消される眼を言います。 　望遠鏡や双眼鏡の接眼レンズの焦点距離が25�oであったとすればこの接眼鏡は+40Dです。-2Dの近視の人は仮想の凸レンズ+2をすでに眼の中に持っていると言えますから、-2Dの近視の人がこの+40Dの接眼鏡を裸眼で使用すれば+42Dの効力がある事になります。すなわち2÷40＝5％だけこの望遠鏡や双眼鏡の倍率が上がる事になります。実は、望遠鏡や双眼鏡などの倍率は、使用する人や見るものの遠近などの条件によって微妙に違うのです。 　一般的に望遠鏡や双眼鏡の倍率は、対物レンズの焦点距離÷接眼レンズの焦点距離とされ、弊社でもお客様にそのようにご説明しております。実は、厳密な倍率の計算式はそれぞれのレンズの前側、後側焦点距離などの数値や観察条件などの数値を使った面倒な式（ここでは省略させていただきます）で、前述の式は一定の条件下で簡略化したものなのです。ちなみに、近視の人が望遠鏡を使った場合、倍率が微妙に上がる、とご説明いたしましたが、遠視の人は逆に倍率が微妙に下がります。また近距離の物体を望遠鏡などで見た場合、倍率は微妙に上がります。 　※ディオプタ−(diopter)とはレンズの焦点距離をメートル測った数字の逆数。